Covariational reasoning

What does research suggest about covariational reasoning?

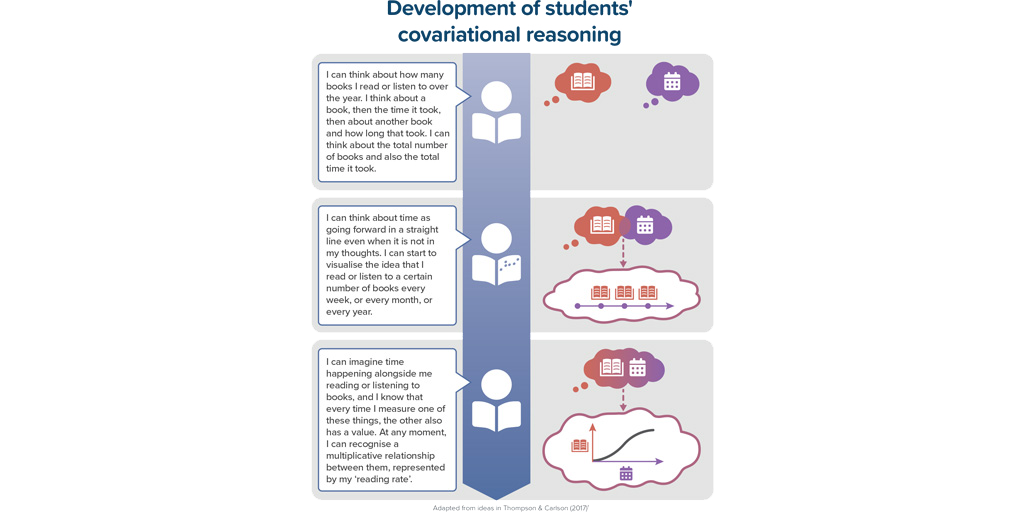
Covariational reasoning can be explored across the breadth of mathematical activity from early primary onwards
Students can be given opportunities to develop covariational reasoning through exploring linear functions and rates; making and critiquing statements; and considering association, correlation and scatter plots
Focusing on plotting or comparing pairs of values may limit opportunities to develop covariational reasoning
Covariational reasoning in statistical contexts requires students to also coordinate the idea of signal and noise, and this can be challenging
It may be beneficial for students developing covariational reasoning to use either time or a counting sequence of numbers as the second variable
Exploring covariation through multiple representations is important; students may find it easier to use graphs at first, especially non-standard ones
Useful activities might include highlighting fallacies and misconceptions, using modelling, and using real data and/or familiar contexts
Software tools can be used to support students’ exploration of covariation by allowing more time to focus on exploring patterns

View Espresso