Teaching and learning equivalence

What does research suggest about teaching and learning equivalence?

Equivalence can be understood as a relationship between two things that can be swapped for one another for a specific purpose
Equivalence is not just part of learning in number or algebra; it is useful across mathematics, although it is also context-dependent
An understanding of equivalence involves using it to solve problems, to maintain balance or equality, to comprehend something differently, and using the equal sign as a symbol of a relationship
Understanding equivalence can be supported by recognising that objects and processes in mathematics can be represented in interchangeable ways, and recognising when they are not equivalent
Noticing equivalence allows students to substitute one form or representation with another, which helps to solve a problem, including simplifying
Students can learn about equivalence from a very early age, and supporting students in understanding equivalence increases mathematics achievement
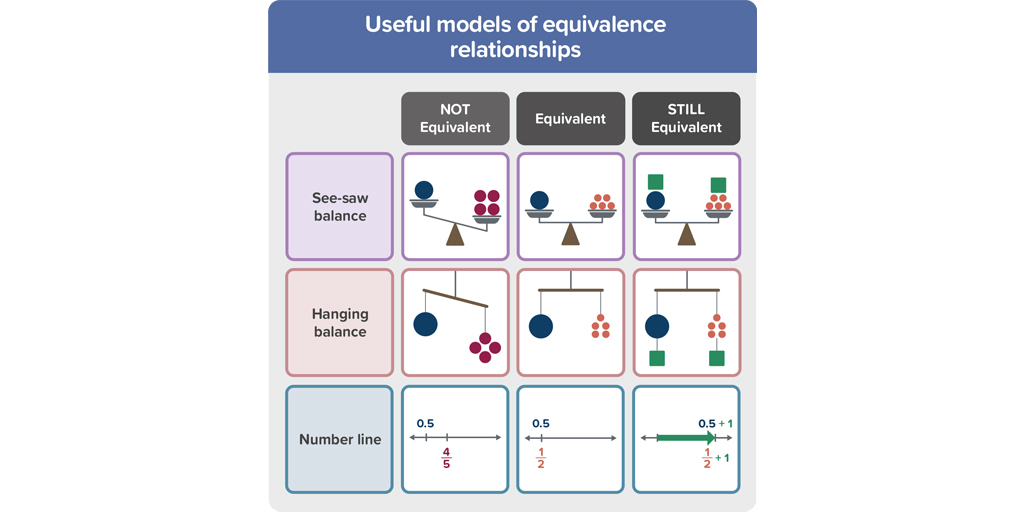
It is suggested that students use the balance principle (either see-saw balance or hanging balance) and number line models to support exploration of equivalence, as well as searching for similarities between processes (as in the infographic)

View Espresso