Early development of functional thinking

What does research suggest about the early development of functional thinking?

Functional thinking is one important strand of early encounters with algebraic ideas, emphasising, justifying and reasoning with relationships and working with different representations of them
Functional thinking involves exploring recursive patterns, covariation and correspondence by considering relationships between two data sets
Children as young as 5 can enjoy opportunities for functional thinking
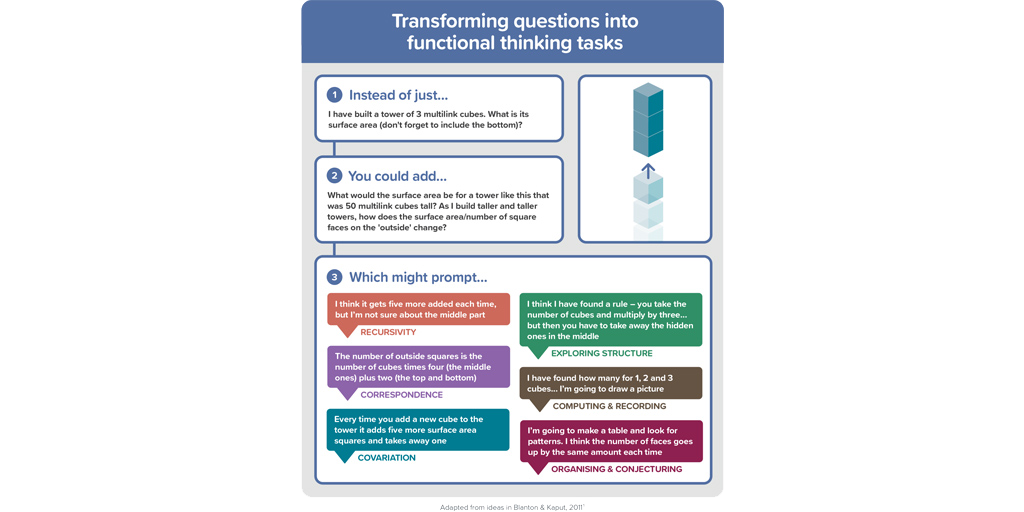
When developing functional thinking, it is useful for students to work with generalising growing patterns using number cards to show position, and also using context (such as children’s literature), multiple representations and technological tools
Functional thinking in mathematics may not be well understood by teachers, so good-quality professional learning is needed, helping them to explore tasks as learners and then as teachers, and using diagrams and images wherever possible
It is helpful in developing functional thinking to help students express relationships in words, tables (especially t-charts), diagrams, function machines, graphs and symbols (both conventional and invented) and reasoning with them, as well as moving between them fluently

View Espresso