12 April 2022
What does research suggest about the teaching and learning of division and multiplication?
- Consideration needs to be given to the ways in which multiplicative reasoning is different from additive reasoning
- Students’ conceptual understanding of multiplicative reasoning is supported by composing and decomposing numbers through ideas of splitting, scaling and replicating
- The array is a particularly useful representation of division and multiplication as it captures two distinct inputs and can reveal commutative and distributive properties
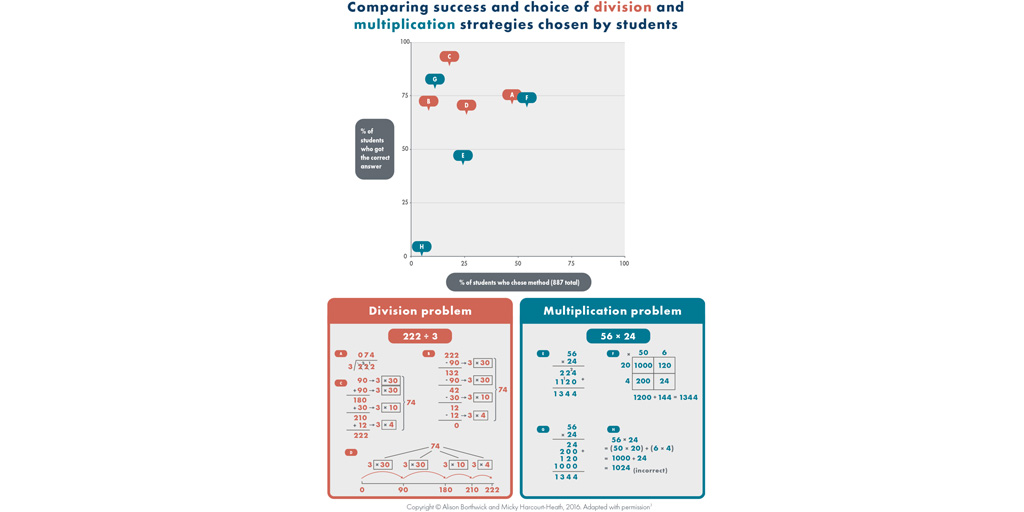
- Exploring a variety of calculation strategies can support students in solving problems flexibly; it follows that it is useful to support this with ways of assessing division and multiplication that allow students to show their flexible knowledge of procedures and ability to choose strategies
- “Chunking” strategies for division (see infographic B and C) support students’ mental methods
- It is suggested that students explore the concept of leftovers or remainders from the outset of their learning around concepts of division
- Developing students’ thinking through the use of the array, an area model and the grid method for multiplication supports understanding of the two-dimensional structure of multiplication
View Espresso