01 July 2020
What does research suggest around the introduction of combinatorics (often called combinations)?
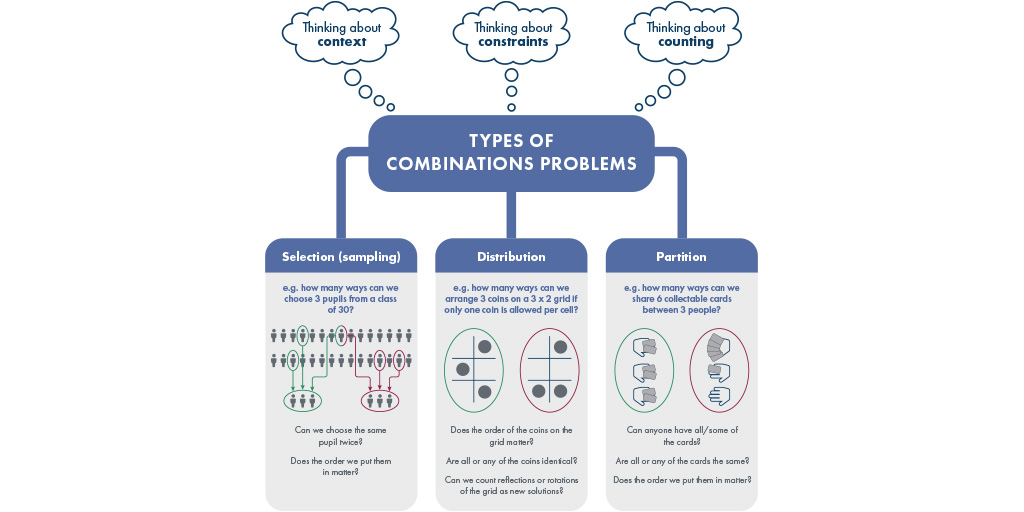
- Early combinatorics, often simply called combinations, is an accessible mathematical topic even at the primary level, because it is based on simple but important ideas of counting, especially the counting unit
- Using the fundamental counting principle and asking important questions about what to count and how to represent the count is important in early development of combinations
- Combinations-type problems can often be rooted in meaningful and real-life contexts and this, supported by the use of manipulatives and representations such as lists, diagrams and tables, can allow students to solve them more effectively
- Combinations problems support development of and connections between varied mathematical concepts
- Solving combinations problems particularly supports the development of logic and early proving
- Students should be encouraged to work towards using pattern and structure when solving combinations problems, eventually being able to work systematically
- Combinations problems may allow students multiple opportunities to begin to conjecture and to generalise, supporting later work on relationships and functions
View Espresso