21 December 2021
What does research suggest about the teaching and learning of fraction equivalence?
- Students need equivalent fractions to understand fractions as quantities, but this can be challenging because “equivalent fraction” can mean the same label for different amounts or a different label for the same amounts
- Students should not just multiply and divide equivalent fractions, but use different area, collection and number line models, flexibly composing, decomposing, partitioning and repartitioning them
- It is recommended that students are provided with opportunities to represent equivalent fractions in different ways, such as pictures, pie charts, ratio tables, fraction bars and double number lines, and in particular to create their own representations
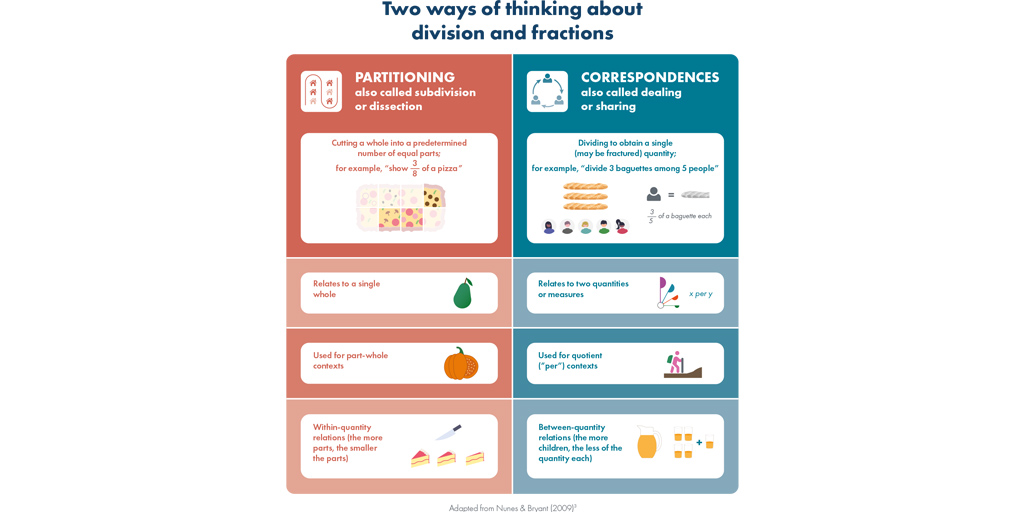
- Focusing on partitioning with students in early work on fraction equivalence may cause difficulties; a correspondences approach is suggested instead
- Modelling decimal equivalence can help students to see that renaming a quantity does not change its size
- To develop fraction equivalence, students should have opportunities to explore constructing, manipulating and mentally repartitioning diagrams, including those where the parts are not equal, and using diagrams which represent examples such as ½ = ½ as different shapes
View Espresso