Teaching and learning of percentage

What does research suggest about the teaching and learning of percentage?

Percentages are commonplace but are an under-researched representation of proportion
Approaches grounded in proportional reasoning with real-life examples are recommended over those that are procedural or atomised
A good grounding for early percentage thinking involves comparison, correspondence and considering “so-many-per-so-many” situations, working on fractions first so that students can visualise percentage as parts-per-hundred
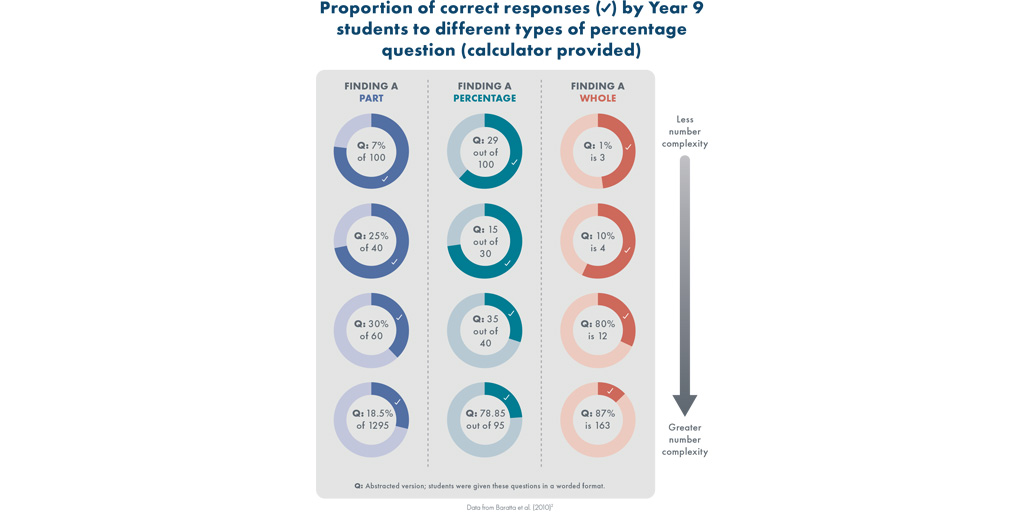
Students may be asked to find a percentage part of a whole, represent a part of a whole as a percentage, or find the whole when given a percentage part; this last is often the hardest for them
Students also find dynamic modelling of percentage change difficult as it involves change in what constitutes the “whole”
It is suggested that early opportunities to develop and explore percentage benchmarks of 1, 5, 10, 25, 50 and 100 are beneficial
Students should have opportunities to move flexibly between representations such as the bar, ratio table, double number line, and their own representations of percentage

View Espresso