Imagine that you, or your students, have been presented with the following task:
Using this design, work out the total number of circles for a similar coaster with 47 circles on each edge.

Which of the responses given below would you instinctively call ‘algebra’?
2𝑥 + 2(𝑥-2)
2 × 𝑥+2 × (𝑥-2)
Two lots of 47 blue circles plus two lots of 45 red circles.
The total number of circles is two lots the number of circles on an edge (blue) plus two lots of two fewer than the number of circles on a side (red).
(This task and the sample responses are taken from Britt & Irwin, 2011)
Did you instinctively pick the symbols?
When asked to make a quick decision in this way, many people will select the examples that contain alphanumeric symbols – this is certainly the way in which many children think of algebra.
If this was the case for you, how strongly do you feel that the other examples are NOT algebra, and why? Do you feel that they are nearly algebra? Could you say that any of the children who created these examples were doing algebra?
This is a fascinating activity that really forces you to confront your preconceptions – I found myself placing all of the above examples into a category called might be algebra, because in order to make a stronger judgement I wanted to know the context in which they were produced, and I want to know what was said aloud but not captured on paper.
I came across the following diagram in a paper by Russell et al (2011). It was created by a child, Laura, in response to the question: How do you know that 16 + 16 = 15 + 17?
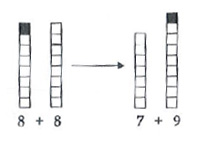
Take a careful look at it and consider the dialogue that may have accompanied this as an explanation to her peers or her teacher. Do you think that Laura is doing algebra? Is she thinking algebraically?
I thought this was a particularly lovely example. At first glance it is easy to value Laura’s attempt to use a concrete representation and to perhaps go further and assume that it illustrates a strong conceptual understanding of additive compensation. But look more closely and there’s even more to notice – while she has chosen to represent a specific numerical example, it is a different example to that in the original question. Is Laura in fact illustrating that she recognises this as a generalised property of addition? Does her choice of numbers indicate that she recognises the process of additive compensation in cases of the form n + n = (n-1) + (n+1), but perhaps not those of the form a + b = (a – n) + (b + n)?
I can’t pretend to have definitive answers to these questions, nor do I necessarily think there are (or should) be any, but they are certainly interesting to consider – particularly in light of judgements that teachers are required to make about students’ capabilities without always having the time and space to uncover their thinking.
Consider now the related task below (presented in a paper by Britt & Irwin, 2011).

Is someone who is doing this task doing algebra? At what point does algebra ‘happen’ in this task?
Three attempts at the task are shown below – how does this affect your thinking?
It’s interesting to think about what feedback you might give these students, and what you might ask each of them to do next. At what stage in their education is each student, in your view?
The challenge of picking apart the notion of algebra and/or algebraic thinking in school mathematics is of particular relevance as we consider the most appropriate way to represent these aspects of mathematics in the Cambridge Mathematics Framework. We value, and want to make explicit, connections between ideas in maths and algebra is something that feels inherently connected to typical topic areas of number, geometry and statistics. But when could (or should) we start to ‘teach’ children to do algebra or to think algebraically and how can it be done as a part of a coherent story of mathematics? While we continue to work on this, do comment below or tweet us @CambridgeMaths.