You are playing a card game. The shifty-looking person running the game says you must choose a card at random. You win if you turn over a card with a picture, and lose if you turn over a card with a number. They claim you have a 50:50 chance of winning on any given turn, but you take six turns and only win once. You feel your blood pressure rising. How might you prove it’s a scam?
The first method that might spring to mind, and the approach students are more normally exposed to, is to use a hypothesis test to ask the question “What is the probability of the data occurring, given a particular hypothesis?” Intriguingly we can reverse this and ask the opposite question: “What is the probability of a hypothesis, given the data?”
The branch of analysis that arises from the latter question is known as Bayesian statistics and it is bizarrely absent in most statistics curricula. This is probably a quirk of the ways in which curricula evolve: historically, the “subjective” Bayesian approach has faced a great deal of scepticism from the “frequentist” establishment. Although Bayesian approaches are now fairly common in applied statistics, and in particular in commercial settings, statistics curricula have not reflected this paradigm shift.
Luckily there are rich opportunities to expose students to some of the early ideas that form the foundations of Bayesian analysis using topics currently in the curriculum, and in doing so we can provide more meaningful opportunities to practise important skills in a modelling context. Let’s return to our card game and see what this might look like in practice.
The Bayesian approach suggests that for our data we can test the likelihood of the hypothesis being true using the binomial calculation:
where n is the number of trials, r is the number of successes and p is the probability of winning (turning over a picture card).
In this example, n = 6, r=1, and p = 0.5, so putting this into the formula gives:
So effectively a 10% likelihood that the claim of a 50:50 chance of winning is true. Would this be enough evidence that the person running the game was lying?
With this basic principle established, there are several ways the idea could be explored further and more dynamically. Firstly, how does changing the amount of available data change the conclusions one might draw? Imagine playing the same game but cumulatively evaluating the 50:50 claim after each go. On the first go you turn over a numbered card and lose. Putting this into the formula tells us that the likelihood the 50:50 claim is true is 0.5 – so far so good. A second go results in a win, so you now have 2 attempts with one success, and the formula gives you a likelihood of 0.5 again. So do you believe the claim at this point? Continuing this process of adding a new piece of data and recalculating gives you a set of results that may look something like:
| Turn |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Result |
L |
W |
L |
L |
L |
L |
L |
L |
W |
L |
| Total wins |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
| Likelihood of hypothesis being true |
0.5 |
0.5 |
0.375 |
0.25 |
0.156 |
0.094 |
0.055 |
0.031 |
0.070 |
0.044 |
Graphing these results gives a clear demonstration of how our trust in the claim may change as more data is added:
Even when you do get a second win, by this point you may have a very low trust in the claim of a 50:50 chance of winning, and this additional success has only a small impact on the likelihood of the claim being true at this point. The act of constructing the table, however, creates multiple opportunities to work with the binomial calculation in a contextual way, and further exploration could prompt students to invent their own hypotheses about the probability of success in the game and test these against the same data to try and decide if there are any claims which are more plausible. This kind of activity also supports a deeper conception of the law of large numbers and a consideration of what “enough” data is in a given context.
Having convinced ourselves that we were getting scammed and the 50:50 chance of winning claim was not true, we could consider what the chance of winning might actually be. In order to do this, rather than testing the data against a claimed probability, we could consider the probability as a variable, and using the data from the game (2 wins from 10 goes) plot the graph of the equation below:
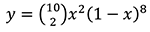
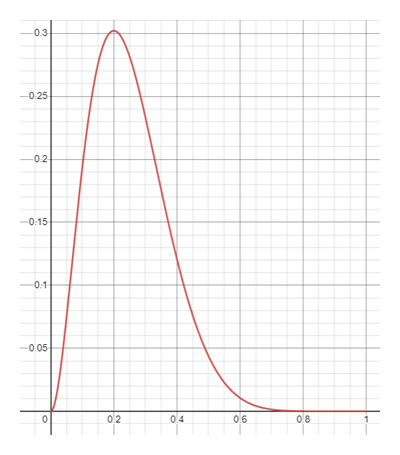
This generates something called a “likelihood distribution” for which the possible probabilities of success from zero to one are plotted on the x axis, and the height on the y axis is the likelihood of the corresponding x value being the true probability that resulted in the generated data. The peak of the graph corresponds to the relative frequency that students are familiar with, but the shape of the graph gives an indication of how likely this is relative to other values too, and potentially whether any claims about the underlying probability should be dismissed as almost certainly false. Exploring further, using tools such as Desmos and creating sliders for the values of n and r, can allow you to investigate how the likelihood distribution changes for different data.
Until Bayesian methods have been elevated to their rightful position in school curricula, activities like this can support the type of statistical reasoning that allows students to explore these ideas in informal ways in tandem with the existing curriculum. If you have used this activity or other resources supporting Bayesian analysis in the classroom, please tweet @CambridgeMaths and let us know how it went.