Cavalieri’s Principle and how it could transform area and volume

As I work through a multitude of ways of introducing mathematical concepts I have happened upon something called Cavalieri's Principle. It's an idea that I have used without realising it, but certainly not to its full capacity.

Take a pack of playing cards in a nice neat pile. What can you say about every card and the pack? First: they all have the same width and length and (since I've got a nice new pack, not ones I've tried to shuffle) it doesn't matter where I measure the width, height or length: they are constant. Finding the area of one card or volume of the pack wouldn't cause too much of an issue.

What would the long side elevation look like? Easy - a rectangle.

Now shear the pack- in other words leave the bottom card but push each one above a tiny distance right (or left, you choose). Now you've got a cross-section that's a parallelogram: a parallelogram prism (try saying that quickly!)

Now here's the fun bit: has the area of the cross-section you were looking at changed?

What about the shape's volume?

Ahh nice! So the shear hasn't affected the surface area of the face we were looking at or the volume of the pack. It might be worth considering what the shear did to all the faces and edges….I'll leave you to think about that one!

Let's concentrate on the parallelogram to start off with. Imagine that that side of the original pack of cards is painted blue. By carrying out the shear the face remains blue and no blue disappears. The new parallelogram has the same height as the original rectangle and no matter where you measure the width it remains constant and equal to the original rectangle; we haven't changed the shape of the individual cards.

Now imagine other shears, maybe a little more imaginatively carried out….so not really shears - more…well, wobbles…

Ok, so the last one is a little trickier with cards but the same principle applies.

In every case if you measure the height or width of the shape between the two edges at a particular point it is equal to that of the original rectangle so is a shear and therefore has the same area as the others.

Now here's the bit that made me go wow… Looking down onto the top of your pack, shear them slightly in the x direction and slightly in the y direction.

So what shape is that? Can you calculate the volume?

It's called - splendidly - a parallelepiped, and has one rectangular cross section (each card). Its other two cross-sections are parallelograms (the two elevations produced by the long and short edges of the stacked cards).

Its volume is exactly the same as the original pack of cards (cuboid), so we can easily find it by finding the cross sectional area (the face of one card) and multiplying by the shape's height.

Now there is only one natural place to go now. Let's imagine we have a pack of cards that are parallelograms of equal area to the original rectangular cards. In other words each individual card has the same base (width) and height as the original pack. Now let's look down on the pack and shear again in the x and y directions. So what shape is that? Does it have a different volume? Can you calculate the volume?

We've made a parallelepiped with parallelograms on every face:

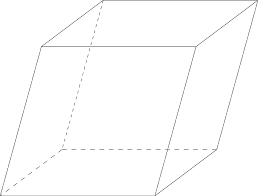
Its volume is the same as the original pack, so yes, we can once again find the area of the base and multiply by the height to calculate the volume. Now that's actually studied in further maths using vectors…but you don't have to be studying further maths or indeed vectors to understand how to do it or actually calculate it given the shape (by measuring) or coordinates of its vertices.

Never again will I talk about a parallelogram as a rectangle with hinges, but instead the cross-section of a pack of cards I shear. Now I'm off to try and find a way to hold a pack of cards in plastic or a pop sock, so that I can shear them in two directions (so I don't have to play 52 card pick up!).

I can only imagine the crazy 3-D shapes that we could produce by using the wobbles above and still be able to calculate the volume! Send in your images and ideas, I'd love to see them.