As I am developing the geometry section of the Framework, I’m working with a philosophy that students need to understand the architecture of shapes; how they are formed and fit together, what similarities hold between different classes and how one shape may be linked to several others by certain properties. In order to analyse shapes students need to be familiar with their make-up in many different senses.
When we’re working with education and mathematical experts we’re often given little gems to go away and think about. The task below is one such gem, described to me by Erna Lampen, from Stellenbosch University, South Africa. It’s one that I believe would be a really beneficial task for students (and teachers) to consider to gain a deeper understanding of the architecture of quadrilaterals and their constituent triangles. Rather than simply starting with a quadrilateral and drawing in a diagonal, this task reverses that process and there is potential to gain a much deeper understanding of the building blocks used to create quadrilaterals.
Take a triangle, any triangle.
Transform the triangle to produce a congruent image that, in place, matches one side with the object to form a quadrilateral.
FOR EXAMPLE
Starting triangle;
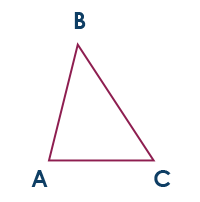
Reflect in side BC to produce a quadrilateral ABA’C.
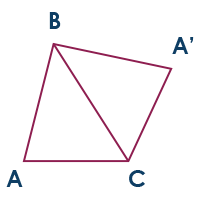
So which triangles, with which isometric transformations (ones that produce a congruent image), produce which quadrilaterals? Can you be certain of your quadrilateral? Are any quadrilaterals impossible to make in such a way?
I had great fun playing around with many different types of triangles: on paper, in my imagination and using Geogebra. Breaking the problems down into many pieces, I was prompted into thinking about other questions:
- What if you allow the triangles to overlap (so long as a quadrilateral is produced)?
- What if you allow a glide reflection (a reflection and translation)?
- What constraints are necessary to ensure you produce a square? A rhombus?
As I’m finding when carrying out tasks such as this, it has the effect of enriching my understanding and appreciation of connections between deep structural ideas in mathematics. Can you imagine ways to show this process using different materials in the classroom? Which ideas about shape might this help students pay attention to (and which might be masked)?
SOMETHING TO TRY:
KS1: Give pupils multiple copies of the same triangle – different groups could have different types of triangle. Using two copies of the same triangle how many different shapes can you make?
KS2: Imagine you have two isosceles triangles. By laying them edge to edge what shapes can you make? Is it possible to make a square? How? Make predictions and then check them. (It is possible to make a square.)
KS3/KS4: Produce instructions on how to construct each type of quadrilateral from a triangle.
KS5: Produce instructions on how to construct a cube frame by transforming the line segment from (0,0,0) to (4,0,0). Can you find multiple ways to do this?
Join the conversation: You can tweet us @CambridgeMaths or comment below.