Intersections: maths and the florist

Claire Curtis is Team Leader of Level 1 Floristry at Capel Manor College, Middlesex.

How would you characterise your current work? 

I have been working as a lecturer at Capel Manor College for 9 years, teaching Floristry to both young and mature students and delivering all aspects of floristry theory and practice to provide skills and an insight into the industry.

How do you feel about maths? 

During my school years, maths was my least favourite subject; like most pupils, I didn’t see a need to learn certain aspects of maths and only absorbed the information I thought was necessary. I believe that one of the main reasons why I didn’t embrace the subject at school was to do with how the subject was taught and explained. I didn’t understand the terminology or the breakdown of how the content was delivered, which led me to feel as though I didn’t really have an interest in learning harder topics. The knowledge that I learnt from school was sufficient for my first job in banking – however it wasn’t until I trained to be a florist that I realised how many different areas of maths are used in the industry and that having a good understanding of maths was imperative.

I have better understanding of how important maths is now. No matter how good your knowledge is on your specialised subject, you can’t achieve the higher qualifications, or often make progress beyond the first levels, without GCSE Maths or English

What is it about your work that is mathematical?

There are many areas of maths that are relevant to becoming a florist, such as percentages so we can calculate profit margins; multiplication, division and addition which are essential to work out quantities and costs of flowers; scale drawings to measure areas so we know where we can place arrangements; and the scale of the designs to how small or large they need to be for the room. Fractions also help us to understand proportions for balance and stability of designs, otherwise they would look out of shape or even topple over.

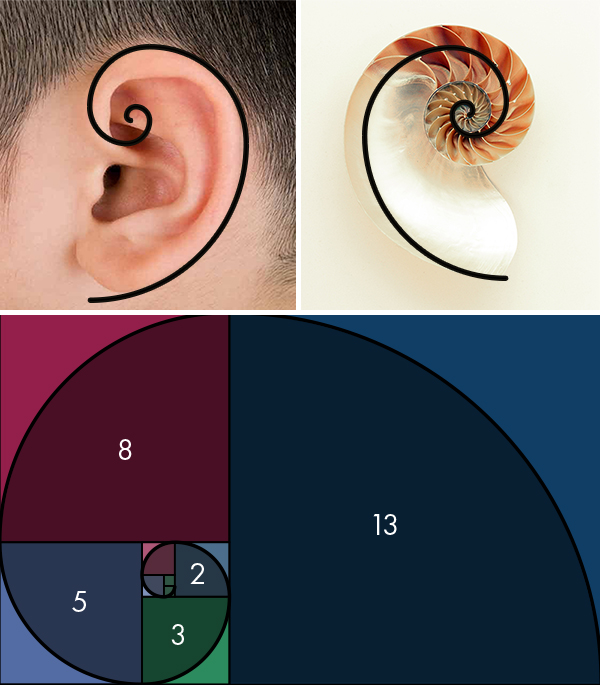
One of the interesting bits of mathematics that I didn’t learn about at school, but which has been introduced to me since working as a floristry lecturer, is the Fibonacci sequence: the numbers found by analysing natural growth patterns increase in the proportional sequence

1. 1. 2. 3. 5. 8. 13. 21. 34. 55. 89…and so on

By adding the last two numbers you obtain the next number in the sequence:

1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, etc.

Below you can see some visual ways these numbers apply in design terms, often appearing as a spiral:

One of the European designs that we create in floristry is called the Form Linear, in which we apply flowers by using the 3:5:8 rule, with 3 main focal groups:

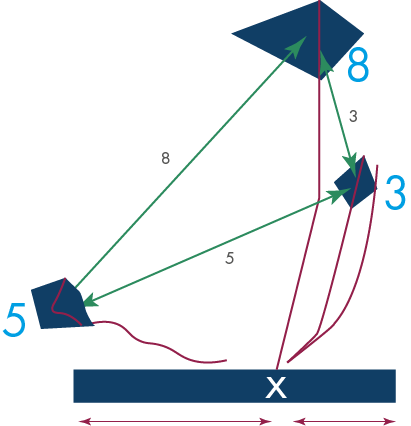
This mathematical sequence is delivered to the Intermediate students as we have learnt that it can be confusing to discuss proportions in this amount of detail to less knowledgeable learners. These proportions are for floral arrangements that we create which have limited materials, placing emphasis on space by purposely creating voids. Although some learners may recognise creating space between flowers is required, they also need to demonstrate an understanding of why the materials have been placed in this particular proportional balance, according to the Fibonacci sequence. The above picture demonstrates how the 8-placement needs to be the dominant group of flowers, with the 3-placement providing a sub dominate of a smaller material showing less form and line. The 5-placement allows the eye to follow the line from the dominate placement by creating a void to another material that will show a contrasting type of flowers. As the chosen materials increase in terms of impact, the form and line appear more dominant, therefore the greater the number becomes along the Fibonacci sequence. It’s quite technical, and very mathematical!

How do you use maths, calculation or numeracy in your work? What tools do you use to help you? 

Calculators are mainly used to help us determine costs of our flowers and designs. As florists, we may need to use tape measures for areas, particularly to help with the scale of room settings and size restrictions. We also use volume – water jugs can be used to measure ratios of flower food against water in order to gain the correct levels to sustain the longevity of fresh materials. Protractors can assist learners to recognise angles, which are important to help with placements of materials within a design.

Do you think maths is creative? If so, how? 

I think maths is most creative if it is linked to a learner’s specialised subject, as it works like a tool and gives them a structure to allow them to explore imaginatively.

Sadly, I can’t remember a creative maths lesson from school – however I do think that creative teaching of this subject would be beneficial to learners. This is an area that is being developed at our college and has proven effective in terms of both engagement and results.

Do you use or rely on any maths that you learnt in school? 

Truthfully, I do not remember any creative or meaningful maths lessons from school. The reason I found maths less than appealing at school is because it wasn’t made clear or relevant to where I might need this in the future or how it might relate to other areas in my life. For example, when a learner is taught multiplication or percentages, it’s really useful to know they would be able to calculate profit margins which might end up determining their salaries!

How would you change the school curriculum, if you had the chance? Why? 

I think the curriculum currently meets the needs of the learners; however, I would like to change the delivery of maths classes to enable the subject to be more relevant to everyday life experiences. For the younger learners, understanding PAYE, P60’s and tax codes seem to be really important for their growth development and will encourage more interest in the subject. It seems common that some students display a negative attitude to this subject, so using ideas and applications that the learner can relate to may help and encourage them to be more focused and retain the information for a longer period of time.

Join the conversation: You can tweet us @CambridgeMaths or comment below.