How did you choose your A Levels, if you did them?
Did you choose to study A Level Mathematics?
Were you tempted to? If not, why not?
According to Ofqual, A level Maths is one of the few subjects that increased in popularity in 2017-2018 (see below)1 and has remained the most popular A level by some margin for several years running2.
2019 data from Education Datalab suggests a dip this year may be at least partly explained by a commensurate overall dip in student entry, as according to their data there were around 3% fewer 18-year-olds in 2019 compared to 2018, although some have suggested the new reformed A level has had an impact
3.
In summary – A Level maths entry appears to be popular and stable. It is also one of the most ‘successful’ A levels – a full 41% of those taking it in 2019 gained an A or A* grade4, which, in context, compares to a mean of 22.4% across the next 9 most popular subjects.
So why are so many students – and indeed adults – still seemingly full of hatred, fear and anxiety around maths? Is mathematics the Marmite of subjects – by the time you reach GCSE, you either love it and feel successful at it or hate it and feel it cannot be part of your identity? If you were to ask a young person whether they chose to study maths post-GCSE, it is my experience that you may well be met with one of two looks: a look of fear or disbelief that you asked the question, or a smile and a look that says “yes, I did and I love it!”. Here are some data that might shed some light on the subject: what do you see here?5
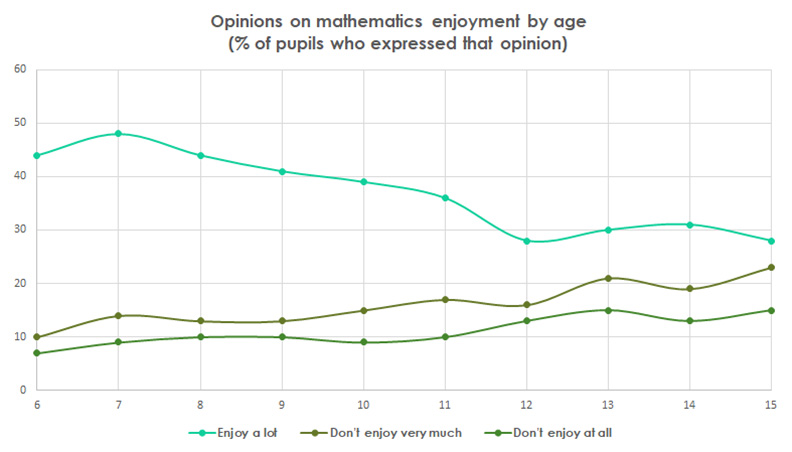
So why is there such discrepancy? One of my own theories as to why students often do not choose to take maths as soon as it stops being compulsory is based on a common psychological model. The CBT model derives from Cognitive Behaviour Therapy and assumes that how we think (our cognitions) influences how we feel (our emotions) and therefore how we act (our behaviour)
6. A student who thinks they are poor at maths or thinks that maths is too hard for them may have negative feelings about maths (maths anxiety, fear) and therefore may avoid maths and not take it further.
Research suggests other reasons why students do not choose to study maths after GCSE. Brown, Brown and Bibby (2008)7 found six main reasons for not continuing with mathematics:
- difficulty,
- lack of enjoyment,
- finding maths boring,
- not needing it for future career,
- not seeing how maths is useful in real life, and
- preference for other courses.
The most common reason for students at all predicated grades (apart from A*) choosing not to continue studying maths post-GCSE was perceived difficulty. The paper7 suggests that sometimes difficulty refers to the anticipated future difficulty and the influence of others on students’ perception of difficulty. For instance, many students think that maths will be very difficult after speaking to older siblings, students who already took their AS Levels or were currently studying the course. Messages from other students, family and teachers can greatly influence students’ perceptions and choice. The authors suggest that this can contribute to students’ low ‘self-efficacy’ in maths or even to some students’ beliefs about personal ‘boundaries’ in mathematics7 (p. 8). If students believe that there are fixed boundaries beyond which it will be impossible for them, they may disengage and not continue with maths. There may also be other barriers created by institutions and curricula7.
Evidence suggests that the majority of students who progress from GCSE to A Level maths are GCSE A* students (73%). Only 34% of A grade students and 6% of B grade students choose to progress8. Can we do something to support students who achieved a B or a C (6-4 in the new system) and would like to continue with maths? I spoke to a colleague of mine who was a maths teacher for 14 years. She gave an interesting suggestion. The school she worked at ran a 3-year maths A-Level, in which the basis (Core 1) was taught across the first year so students who achieved B/C grades could still do maths at Key Stage 5 and develop the skills and understanding necessary for the rest of the course. It seemed to work quite well!
Research7 has identified three potentially overlapping groups of students that could be encouraged to study maths post-GCSE:
- students with grade B, or possibly C, who think mathematics A level is too difficult;
- girls who lack confidence and belief in their own abilities; and
- high-attaining GCSE students who are not very interested in or do not appreciate the importance of maths.
How do we encourage these students to pursue maths further? My colleague’s suggestion is perhaps a step in the right direction, although schools would need to dedicate additional, and scarce, resources to this. Perhaps institutionally some changes could be made to reduce the barriers experienced by these students: for example, enabling those who do not understand the core concepts to develop a deeper understanding of mathematics, which could encourage them and make it seem more possible to continue with maths.
How do we encourage girls who lack self-confidence? We could try by breaking the CBT cycle. This could be done by challenging negative beliefs about abilities and any self-doubt. Every student has bad days – in fact every human has bad days where they don’t perform well at work or school. It is important to recognise potential and encourage students to believe in themselves and their abilities. Albert Ellis’ (1957)9 ABC technique is an example of how challenging negative thoughts could change behaviour.
Adapted from McLeod (2019)
Carol Dweck (1986) suggests that students who view intelligence to be fixed (fixed mindset - “I am not smart”) tend to focus on their performance and its outcome, whereas students who see intelligence as adaptable, flexible and something that can be gained or changed (growth mindset – “I can achieve this if I study and develop my skills”) tend to focus more on development and grasping concepts rather than the final performance outcome10. Research has suggested that the two different approaches may result in different behavioural patterns, with those showing the growth mindset orienting towards mastering and understanding concepts, seeking challenges and persisting when faced with difficulties10. In contrast, learners who show the fixed mindset have been suggested to avoid challenging situations and be less persistent when faced with difficulties10. Dweck’s mindset theory compliments the ABC model, as it suggests that the belief (mindset) is important and should be challenged. As a result, it can in turn affect the displayed behaviour.
Although the proposed theories may not relate to every student and may not explain all behaviours (as is often the case with theories), they may be worth considering when dealing with students who may lack motivation or have set beliefs about their abilities.
How does this relate to your beliefs about mathematics and your identity?
References:
1Ofqual. (2018). Entries for GCSE, AS and A level. Coventry: Ofqual.
2Ellett, P. (2016, April 28). These are the 10 most popular A-levels.
3Jadhay, C. (2019, February 8). New A level maths in 2019. [Blog post].
4FFT Education Datalab.(n.d.). Mathematics A-level.
5YouGov. (2018). YouGov children’s omnibus – subject enjoyment.
6McLeod, A. (2019). Cognitive Behavioural Therapy [Website].
7Brown, M., Brown, P., & Bibby, T. (2008). “I would rather die”: reasons given by 16-year-olds for not continuing their study of mathematics. Research in Mathematics Education, 10(1), 3-18.
8Department for Education. (2012). Subject progression from GCSE to AS Level and continuation to A Level (Research Report DFE-RR195).
9Ellis, A. (1957). Rational Psychotherapy and Individual Psychology. Journal of Individual Psychology, 13, 38-44.
10Dweck, C. S. (1986). Motivational processes affecting learning. American Psychologist, 41(10), 1040-1048.
Join the conversation: You can tweet us @CambridgeMaths or comment below.