Last month, the Guardian reported on the food company Gregg’s marketing strategy regarding doughnuts and calories. This caught my attention, because, as I may have mentioned, stuff about circles and humans is of particular interest to me. Circles are hard. Doughnuts, which (despite the Guardian calling them ‘balls’) I would suggest may be modelled as either cylinders or cylinders-with-cylinder-bits-missing, are particularly hard. What might be the effect of this modelling assumption? Will it result in an underestimate of the dough volume? An overestimate? And would the size of the error even vary consistently for different sized doughnuts?
Before we begin, I wonder if you would like to try ordering these doughnuts from smallest to largest in terms of volume – see if you can do it relatively quickly, without working anything out.1
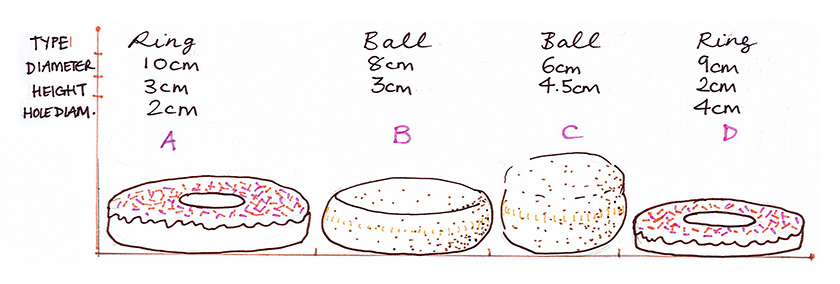
The article suggests Greggs are marketing ring doughnuts as healthier choices to their non-toric cousins based on the calories found in each – a calculation which incorporates both volume of dough and amount of icing used. I liked thinking about icing as a variable, because it is a good way to think about surface area and considering the height at which it stops makes this a non-trivial problem, especially if we conveniently imagine for a moment that the icing only occurs on ring doughnuts. I estimated a doughnut height to be 3cm, icing height to be 1cm, diameter to be 10cm and the diameter of the hole to be 3cm before getting my sticky hands on some nice messy data, and was intrigued to find that I wasn’t too far off, but the hole/doughnut ratio appears to be very much non- standard. Here are a few that I measured, all in cm:
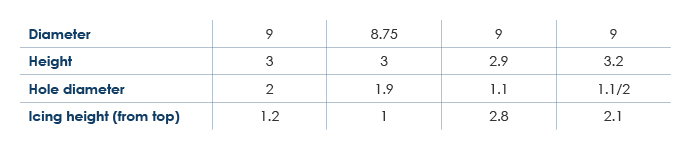
I had an interesting issue here – as you can see from the data above, one of the holes was misshapen, resulting in an elliptical rather than circular shape. Before we move on, you may wish to consider, as I did: Is it possible to find the mean of the two measurements of the diameter here and just use this to model the volume? If so, why? If not, why not?2
But what, I hear you say, about jam? (Indeed, how incomplete this doughnut discussion would be without it.)
From my rudimentary data rummaging, which proceeded in inverse proportion to my stomach rumbling, I found that an ‘average’ doughnut appears to have roughly these proportions:
But when I started to model icing height vs jam filling, I noticed that there was a shortcut – if the calorie content of each is similar enough, it shouldn’t matter what type of doughnut or how much filling is in it – and so, indeed, it turns out. It appears that the effect of jam vs icing may cancel out, essentially because the calorific content of fried doughnut, jam and icing are similar enough for it not to matter too much overall:
Data from https://www.myfitnesspal.com/; something to note here is the wide deviations I found in estimates for these values
This was a sprinkling of good news: a simple model that just considers the volume of dough is most likely valid, meaning I don’t have to get myself into a jam modelling the net contribution of icing.
Question: Have you ever heard of the great Pop Tarts Mystery?
The plot, if not the icing, thickens. In 2009, a blog post asked the question: Why does a single Kellogg's Frosted Strawberry Pop-Tart have 200 calories, while an Unfrosted Strawberry Pop-Tart has 210 calories? Surely, they asked, ‘frosting couldn’t count for negative calories, could it?’
Of course, if maths (and physics) works – no indeed it could not. But it was not until 2015, some 6 years later, that the mystery was finally solved. Kellogg’s confirmed that the unfrosted version has ‘a slightly thicker crust’, and that was that. But why? I leave it to the reader to speculate. But the principle – that leaving off the icing does not automatically mean fewer calories – is an interesting one to consider.
So, returning to the Greggs hypothesis: are ring doughnuts better for you?
Here is a plot of doughnut weight in grams against doughnut calorie value. Five of these data points are ring doughnuts and five are ball ones. Can you predict which data values are which?
What can we conclude from this limited data? Are ring doughnuts better for you? What do you think?
References:
1The correct answer is : D (approx. 102cm3), C (approx. 127 cm3), B (approx. 150cm3), A (approx. 226cm3). Did you get them right?
2It is not, at least if you are using the arithmetic mean (add the two values and divide by two). This is because the area of an ellipse (and indeed any 2D shape) is two-dimensional, and in this case is found by multiplying the two lengths (width and height from the centre of ellipse) and then multiplying by π.
Join the conversation: You can tweet us @CambridgeMaths or comment below.