I have been thinking about proof for many, many years now (at least a decade. Maybe two. Maybe three…).
Test Dynamic Content
So instead of writing, meandering around some idea, here’s a visual selection of some of my favourite geometrical proofs ever… the question is, can you identify the theorem or what they prove?
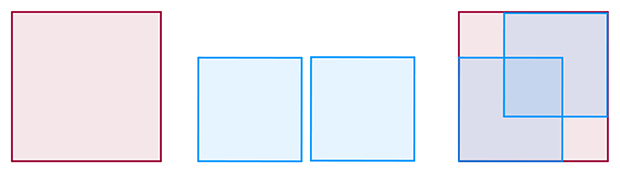
The area of the large square is double the area of the small square; the square’s side lengths are the smallest possible co-prime pair.
You can tweet us the solutions @CambridgeMaths or comment below, and feel free to send us some of your own geometrical proofs!
Some ideas for the classroom:
Early years and lower primary
Using link cubes show that
- an even number plus an even number is always even
- an odd number plus an odd number is always even
- an even plus an odd number is always odd
Upper primary
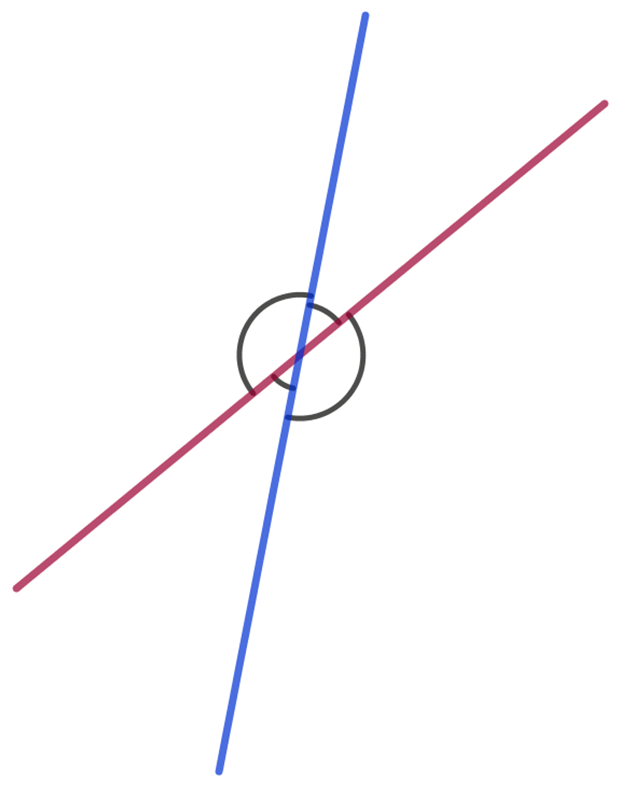
Use this diagram and your knowledge of angles to explain why vertically opposite angles are equal.
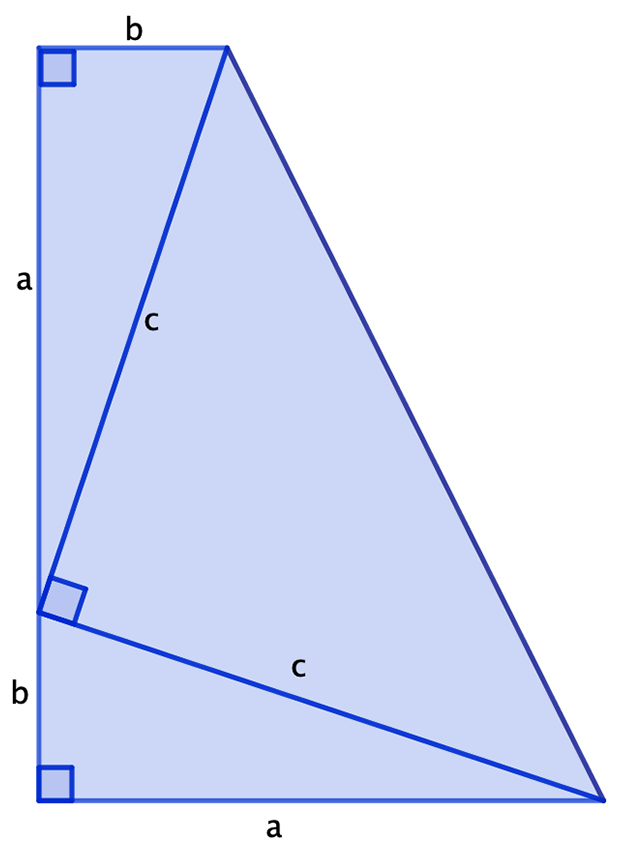
Early secondary
Find two different ways to express the area of this trapezium to prove Pythagoras’ theorem.
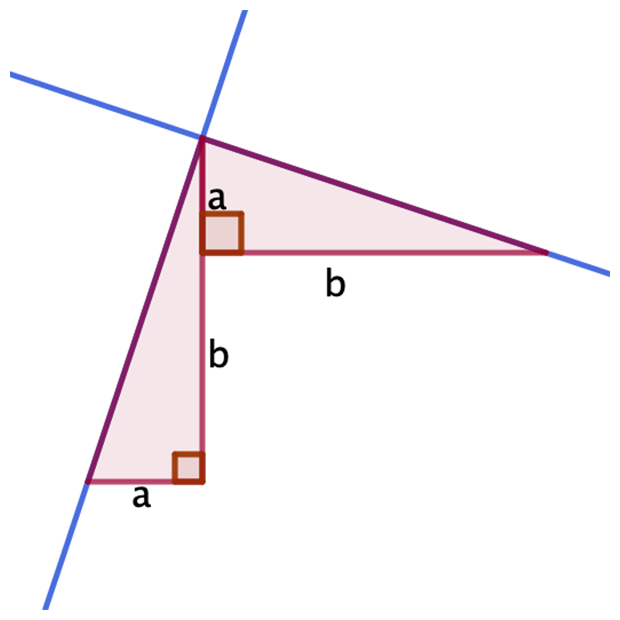
Upper secondary
Use the diagram below to help explain why the gradients of perpendicular lines are negative reciprocals of one other.