Talk to the vast majority of people about the maths they learnt at school and they’ll remember Pythagoras’ Theorem – even if only by name, and even though it is seriously doubtful whether it should be attributed to Pythagoras at all. This theorem is named after the Greek mathematician and philosopher, Pythagoras of Samos (circa 500BC). There is doubt as to whether he proved the theorem and evidence that it was actually known (in some form) by the Babylonians a thousand years earlier, and in India somewhere between 800 and 400BC.
Nevertheless, it’s a wondrous piece of mathematics with umpteen lovely explanations that can be investigated from quite different angles – allowing pupils to build up a repertoire of different representations that they can move between flexibly.
Here’s a few explanations (I’m avoiding the word proof right now while reading more about its use) that I’ve come across through reading, talking and pondering ideas. Do you have a favourite? Please do add your own!
Method 1: In discussion with Prof Martin Hyland
This explanation relies on understanding of scale factors of area.
You should be able to identify three similar triangles; one with hypotenuse a, one with hypotenuse b one with hypotenuse c. The sum of the areas of the triangles with hypotenuses a and b equals the area of triangle with hypotenuse c.
Area of triangle on c = area of triangle on a + area of triangle on b
If we’re talking about a relationship between the areas of the three similar triangles we could consider any three similar shapes linked by edges a, b and c. It could be that a, b and c are sides of three equilateral triangles,
Hence
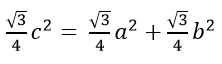
or three diameters of three semi-circles,
Hence
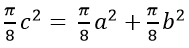
or even the sides of three squares.
Hence
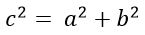
Method 2
A more formal explanation using scale factors.
Three similar triangles. △1 with hypotenuse a, △2 with hypotenuse b, △3 with hypotenuse c, with scale factors such that
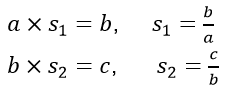
area of△1 x s12 = area of△2
area of△2 x s22 = area of△3
area of△1 + area of△2 = area of△3
area of△1 + area of△1 x s12 = area of△3
area of△1 + area of△1 x s12 = area of△2 x s22
area of△1 + area of△1 x s12 = area of△1 x s12 x s22
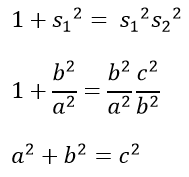
Method 3
Another method using the equality of ratios of sides in similar triangles.
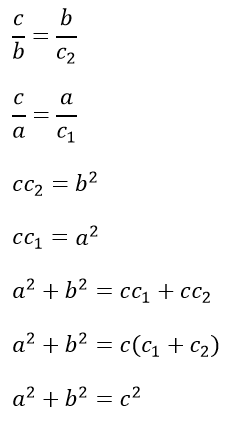
Method 4
Finding and equating two expressions for the area of the shape below (there are lots of versions of this style of explanation).
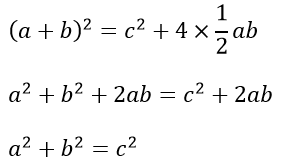
Method 5
Translating the four right-angled triangles in a square frame.
If four right-angled triangles as shown in the left-hand picture are moved around (translated) in the same square frame so that they make up two rectangles as in the right-hand picture, the rest of the space remains unchanged, but is clearly shown as c2 on the left and a2 + b2 on the right, demonstrating their equivalence.
Method 6
My personal favourite: using shearing, rotation and equality of area.
and repeat for the other square on the non-hypotenuse side of the triangle…
No matter how you approach Pythagoras’ theorem there are so many ways to explain the ideas and structure at work here. Importantly, every one of these discussions emphasises the fact that we’re talking about a relationship between areas. We then use this relationship to find missing side lengths. How do you treat this topic and what’s your go-to explanation of it?
I’d love to hear of your favourite explanation, demonstration or approach to Pythagoras’ theorem.
Join the conversation: You can tweet us @CambridgeMaths or comment below.