Count – out loud if you can – from 1 to 20.
Now do it again, but try to think about the mental image that is formed in your mind when you do so.
What do you see?
I was asked this question some time ago and quickly responded that I saw the numbers on a horizontal line, increasing from left to right. The friend asking me this was intrigued and wanted to know more so I continued, trying to describe something that I had never really been consciously aware of. I explained that, as I count, I am mentally ‘hopping’ or ‘sliding’ along this line, so saying ‘1, 2, 3, 4, 5’ conjures an image a bit like this:
I was encouraged to give more detail, so I continued that I feel as though I am simultaneously holding information about the starting position (1 in this case) and the direction of travel (right in this case) during the counting process. The number that I am ‘perched on’ at a moment in time is in particularly sharp focus with surrounding numbers slightly fuzzy or perhaps greyed out.
At this point I stopped. I was trying to describe something imaginary and elusive and, as I tried to pin it down, I ended up questioning what I had drawn. After some thought I changed my description: actually my mental number line is increasing vertically, from the bottom up, like a thermometer. But it feels like things happen around the 10s, they seem to stand out, and I think that perhaps it becomes horizontal after a while … or maybe on a slope increasing from left to right …

or maybe
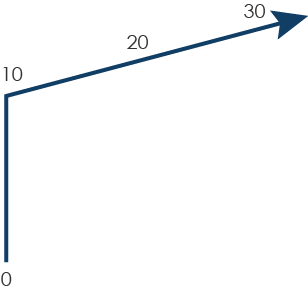
Unsurprisingly, my friend looked confused. Interested, but confused. She said, ‘but, where is this number line that you see?’ I must have looked puzzled because she tried again, ‘You’re looking at me, right? So you see me? But you also see this number line? Is it over the top of me? Is it next to me? Where is it?’
So it turned out that this friend (a mathematician I might add) was so intrigued because she doesn’t form mental images in her ‘mind’s eye’, when counting or otherwise. It’s not because she wasn’t ever introduced to different representations of number or strategies of counting and calculation. On the contrary – an excellent mathematician and educator, she can physically demonstrate multiple representations, images, and diagrams of problems incredibly clearly, using something concrete (perhaps on a whiteboard or paper). But it seems that she doesn’t replicate this kind of image in her mind – fascinating!
So I started asking other people about what they ‘see’ when they count. Many people said a horizontal line, increasing from left to right. A couple however were quite clear about there being ‘corners’ in their number line, and these corners weren’t necessarily located at the 10s as I might have predicted (in one case I was told that ‘you go up, then you turn right at 7’!).
From the perspective of a teacher I find the notion that my students might have completely different mental images of a number line, or none at all, a bit perplexing. I think that I always assumed that students were reconstructing and recalling mental images in the same way that I do and that this reflected what they were able to put down on paper. It certainly makes me think hard about the, perhaps limited, ways in which I tried to support those students who were not secure in counting and arithmetic problem solving.
Research suggests that it is helpful for students to develop good mental models of the number line as part of mathematical intuitions that help ‘to quickly decide that 9 is larger than 5, that 3 falls in the middle of 2 and 4, or that 12 + 15 cannot equal 96, without much introspection as to how we perform these feats’ (Dehaene, 2001, p. 16). However, ‘empirical evidence of a link between the mental number line and higher order mathematical competence is sparse and inconclusive… virtually nothing is known about the relevance of the mental number line for the acquisition of more advanced mathematical concepts’ (Schneider, Grabner & Paetsch, 2009).
Much research has been performed on the way in which mental number lines seem to be arranged, and two clear behavioural structures have emerged: the distance effect and the spatial–numerical association of response codes (SNARC) effect. The distance effect states that numbers on the mental number line are spaced out such that discriminating between numbers near one another is harder when they are closer to one another; there appears to be a logarithmic relation between the numerical distance and reaction time (Dehaene, Dupoux, & Mehler, 1990). The pleasingly-named SNARC effect shows another behavioural indicator of a mental number line: people being tested tend to respond to smaller values faster with their left hand and to bigger values faster with their right hand when comparing numbers with a reference number, suggesting a correspondence with a left-right number line for most individuals. Interestingly, the effect does not reverse for left-handed participants, or when participants perform the task with the hands crossed (Dehaene et al., 1995). However, for those who use a right-to-left writing system the opposite effect (reverse SNARC) seems to present (eg Dehaene, 1993, Zebian, 2005).
So, what do you see when you count to 10, 20, or 100?
References:
Dehaene, S. (2001). Precis of “the number sense.” Mind and Language, 16, 16–32
Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122, 371–396
Dehaene, S., Dupoux, E., & Mehler, J. (1990). Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. Journal of Experimental Psychology: Human Perception and Performance, 16, 626–641
Schneider, Grabner & Paetsch (2009) Mental Number Line, Number Line Estimation, and Mathematical Achievement: Their Interrelations in Grades 5 and 6. Journal of Educational Psychology, Vol. 101, No. 2, 359–372
Zebian, S. (2005). Linkages between number concepts, spatial thinking and directionality of writing: the SNARC effect and the REVERSE SNARC effect in English and in Arabic monoliterates, biliterates and illiterate Arabic speakers. Journal of Cognition and Culture, Special Issue: on Psychological and Cognitive Foundations of Religiosity, 5(1-2), 165–190
Join the conversation: You can tweet us @CambridgeMaths or comment below.