It’s been a huge few weeks in global, with the US election results dragging out over several days, causing many people to ask the question “Why is it taking so long to count?” – and others, notably the incumbent leader, suggesting that the count should be stopped when the results were satisfactory in their view. It has never been clearer to me that even that most simple of mathematical processes, the count, is full of important decisions. For example:
- Is the thing you are counting a physical object in front of you, a representation of something, a symbol, an abstraction, an object of enquiry, or a combination of things, or something else?
- How do you know when to start counting?
- How do you know when to stop?
- Which things are distinct things to be counted and which can be combined, either in terms of counting as one thing, or in terms of making the count quicker by multiplying instead of adding?
- Does the order in which the things are counted matter?
- How are you checking your count?
We have seen issues inherent in all of these questions played out in the news. For example, the order in which votes came in from different states – while not making any difference to the overall total, when it eventually arrives – changed the narrative of the presidential race and placed the focus on particular states, such as Georgia and Pennsylvania, as crucial turning points. Below you can see one way of visualising this:
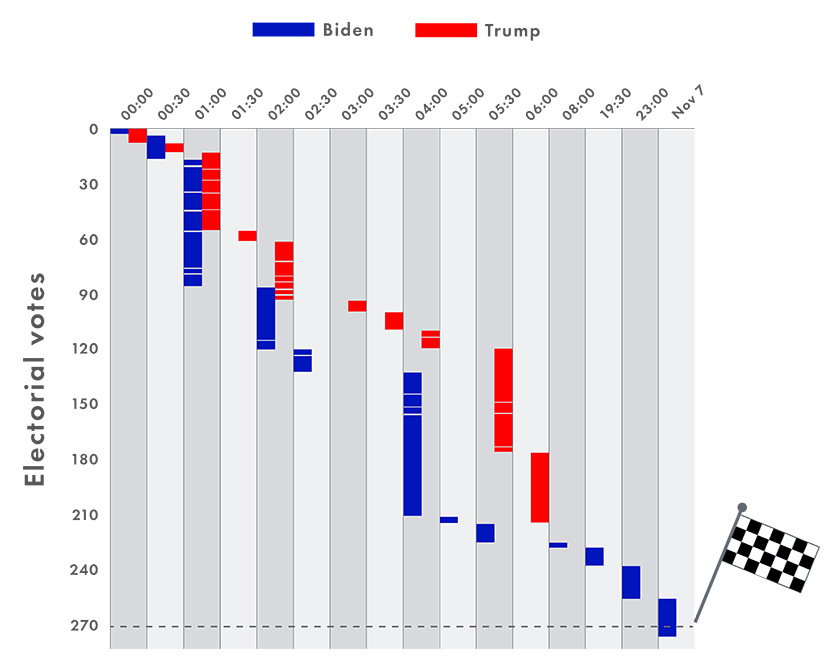
There is also the key question of what we choose to count at all. Political voting systems, at least democratic ones, suggest every person should get a single vote, and they should all be counted together carefully to compare popularity of candidates. In the USA, the system is quite complex: each person’s vote (called the popular vote) feeds into the electoral college vote, not always directly (in all states except Maine and Nebraska, the majority of the popular vote determines the electoral college votes outright; in those two, they are allocated proportionally). Electoral college votes are in turn roughly proportional to the population of that state. As you can see, we are beginning to move from the idea of counting to the idea of proportionality quite naturally, by comparing parts and wholes. As my colleague Tabitha often asks me to consider: What is the whole here? Of course, not every person in the USA has a vote that counts – you have to be a US citizen, over 18, and registered; and being a convicted criminal can prevent you from having your vote counted. Only a particular proportion, too, of the whole eligible population actually votes – in this case around 70%.1 Elections, in essence, compare the counted totals of only those who actually voted, which becomes problematic if a small enough proportion of the population vote; this is related to the Law of Large Numbers (as a sample size grows, its measured characteristics become closer to those of the population). And this is just a flavour; many important and varied mathematical principles begin to grow from this very simple idea of counting in the same way.
If you have ever worked with children learning to count you’ll have noticed what a complex process it is, involving much more than just the memorisation of counting words. That is partly because of the complexity of some of the decision points listed above, which may become fluent and automatic over time but which at first require our close attention. In particular, comparing two counts – essentially the basis for any election – involves all of those plus the crucial idea of sameness: whether the two things we are counting are the same in an important way (in the case of voting, if not, then it would not likely be seen as a fair process…). With young children, it is wonderful to watch them begin to practise abstraction by comparing sets of things that may not be the “same” in the physical or visual sense, but can be seen and therefore counted as the same when we understand that the count is a process of disregarding those attributes and focusing only on the discrete sameness of things: the total number of distinct things.
Here is one representation of what some of these interconnected concepts might look like, from the Cambridge Mathematics Framework:
In contrast to many over these past few weeks, given this lovely complexity, I’ve been surprised such an important count hasn’t taken longer!
References:
- https://en.wikipedia.org/wiki/Voter_turnout_in_the_United_States_presidential_elections
Join the conversation: You can tweet us @CambridgeMaths or comment below.