Becoming more than nothing

Is zero a number? Explain. 

Take a moment to think about that question. What do you think your students would say? Do you think the response be the same for a child aged 7 compared to someone at 16, or 19? 

Although we use the symbol 0 all of the time in the ‘real world’, there are still many difficulties that students seem to encounter when attempting to deal with zero in mathematics. 

Distinguishing between the notion of zero as ‘nothing’, and so can be ignored, and zero as nothing-that-tells-you-something, is a very subtle and easily overlooked complication in student learning. 

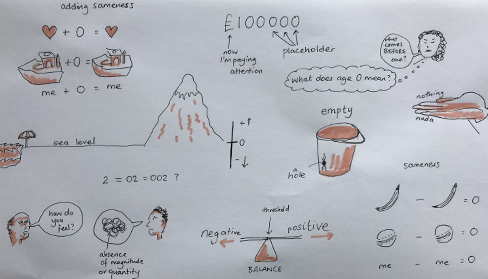
I have unearthed a variety of definitions, or meanings of zero, a selection of which are listed below. Which of these do you like best? Which of them aligns the most with your own ideas, or mental image, of zero? 

1. The whole number between -1 and 1 
2. A number that represents nothing - of something 
3. The symbol 0 denoting the absence of all magnitude or quantity 
4. The dividing point between negative and positive numbers 
5. The result of endless couples of opposites: a + (-a) for any natural number a 
6. The integer immediately preceding 1 
7. The identity element with respect to addition: a + 0 = a 
8. A placeholder in a place-value number system 

It’s interesting to think about when and how each of these might be useful to children learning mathematics, and in turn, which of them are dependent on each other. For example, when children learn the counting sequence, they may encounter 0 as the ‘number’ before 1 (definition 6), or the ‘first’ number in the sequence before they associate those values with quantity or ‘cardinality’. When developing additive reasoning, definition (7) may be important to encounter but relies on some familiarity with definitions (2) and (3). Many ways of introducing negative numbers rely on definition (4) and therefore (6), (1) and (5) to some extent. 

Definition (8) is a special one – it is often one of the first instances of zero that young children encounter, certainly as they learn the counting sequence beyond 9. It relies on definition (2) in particular but is not always seen in that way. The effects of language can be problematic, certainly in English where 10, 20, 30, … have unique number names (ten, twenty, thirty, …) that do not reveal the underlying place-value structure and ‘hide’ the zero. 

The next challenge that we encounter is when we try to operate with, or on zero. In terms of addition and subtraction we can convince ourselves of (7) by extending the same reasoning that we use with the addition and subtraction of non-zero numbers. Maybe we use the image of moving or stepping along the number line, or adding nothing to a set. When it comes to multiplication, something like 4 x 0 may be explained using the idea of repeated addition (we have ‘no lots of 4’), or maybe by observing and extending patterns in calculations like this: 

Or maybe we talk about multiplication as scaling - where 4 x 0 is seen as reducing 4 to zero in the same way that 4 x 2 may be seen as enlarging 4 to something twice as ‘big’. 

And now – hold on to your hats – the mathematical minefield that is division by zero. How do you explain that one to students? This is the point where I feel as though we’re taking a dive down the rabbit hole, as questions such as ‘what is infinity?’ and ‘is infinity a number?’ start to swirl around us! 

One way to approach it might be to ask: what is the same and / or different between these two calculations: 

In one sense here we are asking if there is some number that (a) equals 5 on multiplication by zero; and (b) equals zero on multiplication by zero. This relates to a bigger idea of ‘doing and undoing’ and ‘reversible calculations’ that some consider an essential component of algebraic thinking. 

Perhaps, thinking another way, we might consider the effects of dividing the given value by smaller and smaller numbers, sneaking up on ‘division by zero’ from the side, maybe in the hope that it won’t notice (unfortunately, in this scenario it depends which side we choose to sneak up on, which can be somewhat confusing). However, this way of thinking makes some significant connections to bigger ideas such as asymptotic behaviour and limits, and lends itself to a rather pleasing graphical representation. 

Now, thinking about the ways in which these ‘examples’ may emerge from other mathematical experiences, and therefore how it is natural, convincing and appropriate to explain them in these differing contexts is fascinating. The idea of zero, its many roles and its often unintuitive behaviour seems to be deeply connected to many areas of mathematics.